Excel Value of Continuously Compunded Bond
In this tutorial, we'll explain how to calculate compound interest using the Excel formula with regular and irregular deposits. We shall also discuss how to calculate future values of investment based on daily, monthly, and yearly compounding interest rates.
Firstly, we have to know that the compounding interest rate concept is the center point of the investment world. Basically, it moves the stock market, the bond market, or simply the world. Simply, understanding compounding interest rates can change your behavior with money and savings.
Moreover, the concepts might seem a bit complex for individuals who did not study finance, accounting, or business studies. But if you read this article with attention, your misconceptions will be removed, your understanding will be clear certainly.
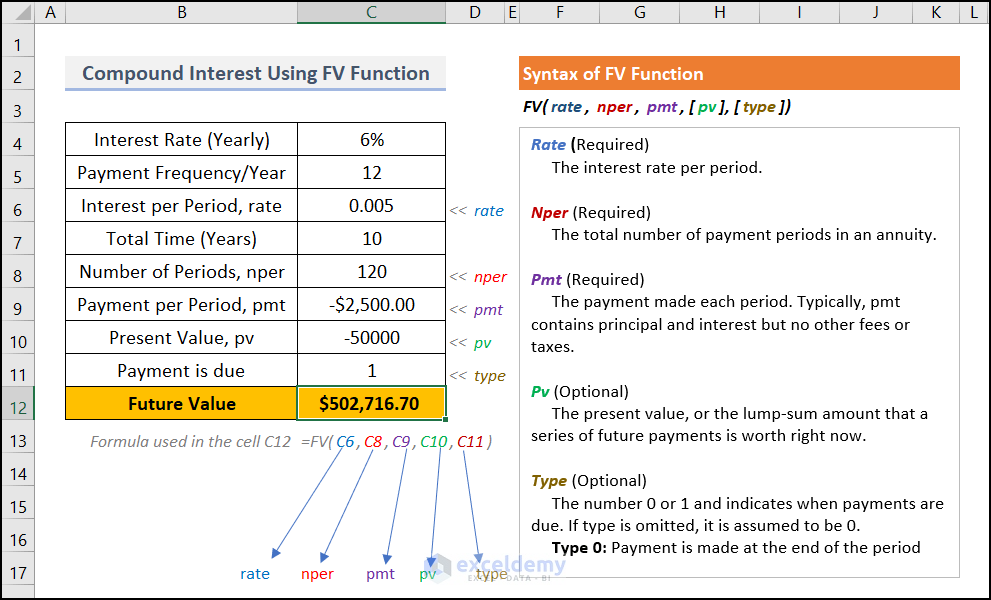
The following image provides an overview of the calculation process of compound interest in Excel using the FV function. Later, we'll show you the process with simple steps and proper explanations.
Download Practice Workbook
Download the following practice workbook. It will help you to realize the topic more clearly.
2 Methods to Calculate Compound Interest Using Excel Formula with Regular Deposits
Say, you're going to run a savings scheme with one of your trusted banks. Here, you want to know what your total amount after a certain period (years) will be. In this case, we will use the Excel FV function. We can also calculate it with Excel formulas.
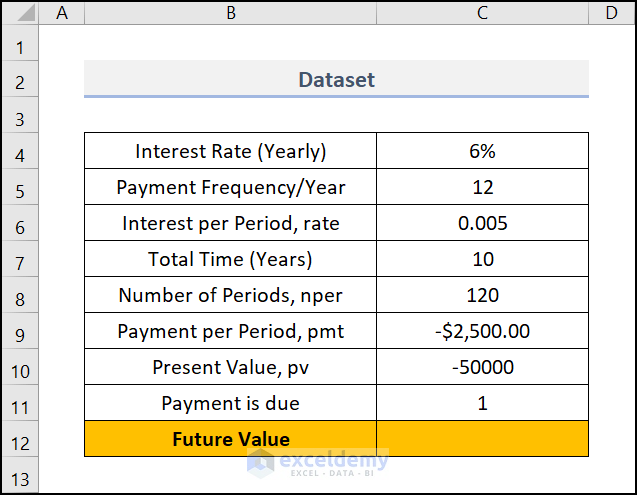
Here, we have used Microsoft Excel 365 version, you may use any other version according to your convenience.
1. Using FV Function
Excel's FV function returns the future value of an investment based on periodic, constant payments and a constant interest rate.
📌 Steps:
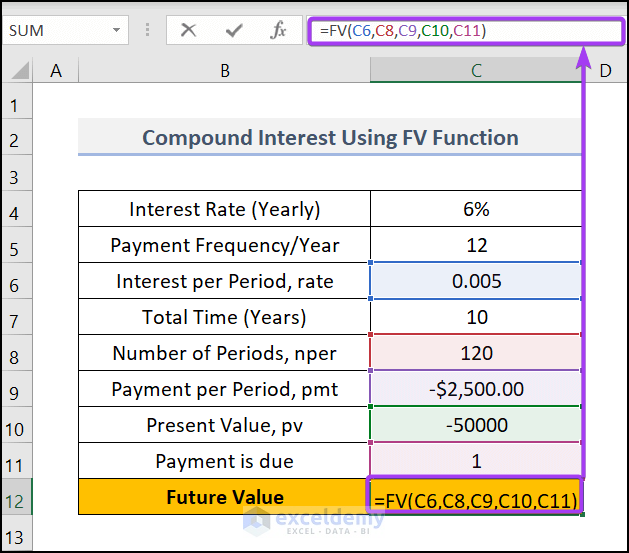
- Firstly, select cell C12 and write down the formula
Here,
C6=Interest Per Period, ( rate )
C8=Numbers pet periods, ( nper )
C10=Payment per period, ( pmt )
C11=Present Value, (pv)
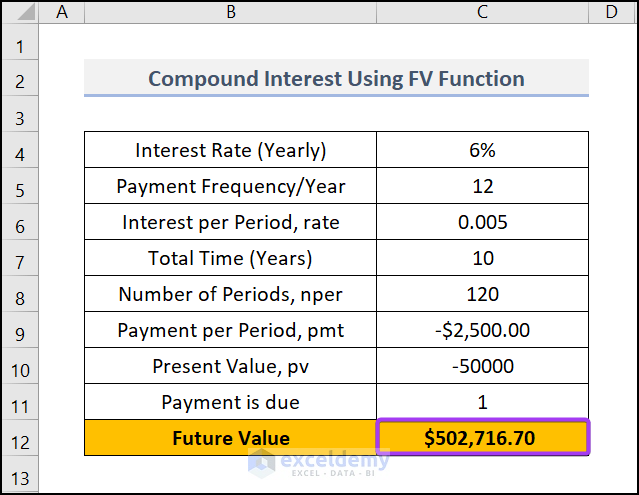
The syntax FV(C6,C8,C9,C10,C11) returns the future value by compound calculation.
- After that, Press ENTER and the formula will display the future value.
2. Calculate Compound Interest with Regular Deposits Using Manual Formula
We can use an Excel formula for calculating compound interest with regular deposits. For this, you have to follow the steps below.
📌 Steps:
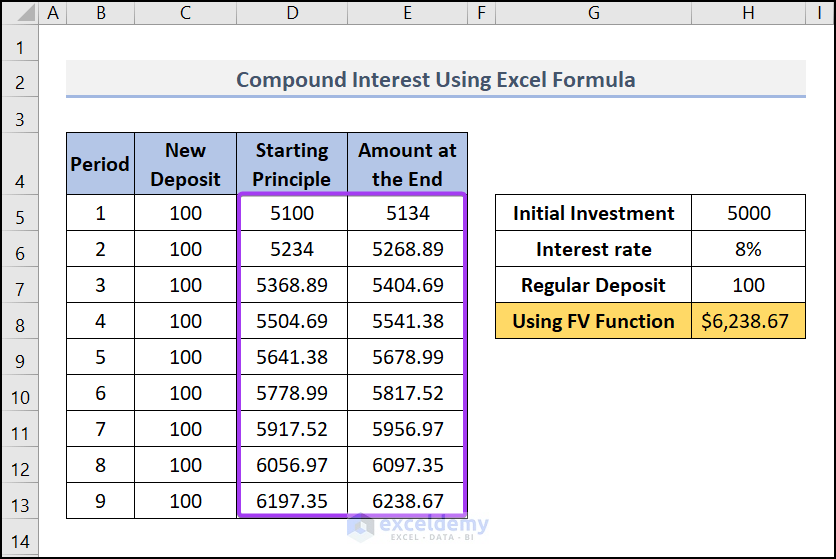
- Initially, we have taken only 9 months or periods (under the Period column). Add more periods under this column if necessary and apply the formulas from the above row.
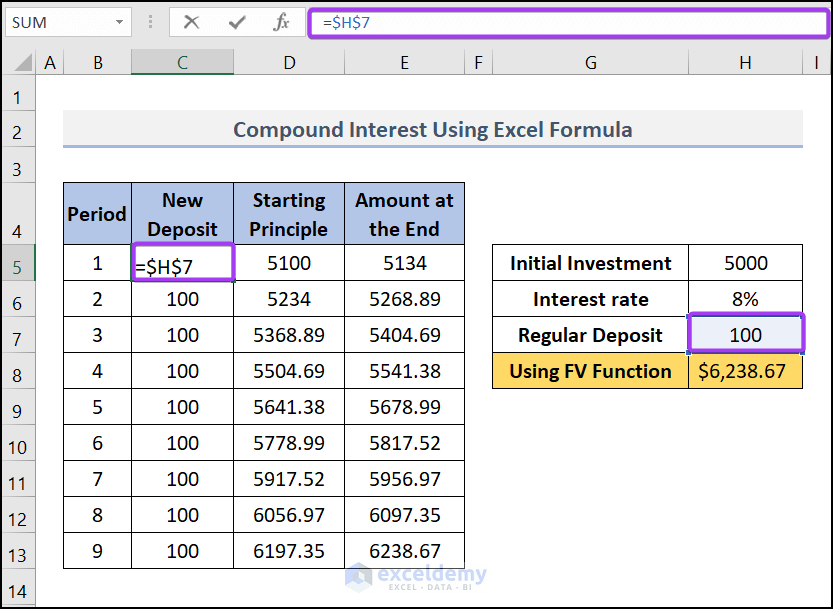
- After that, in cell C5 (under the column "New Deposit"), we have used this formula, C5=$H$7. And then applied this formula to other cells in the column.
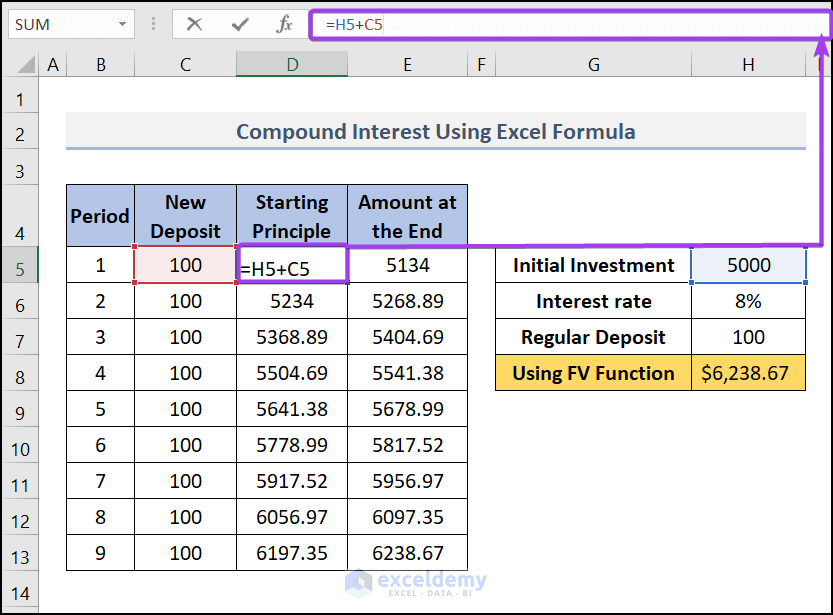
- Then, in cell D5 (under the column Starting Principle), We used this formula, D5=H5+C5. This formula is used just once. This is just to add the initial investment to the formula.
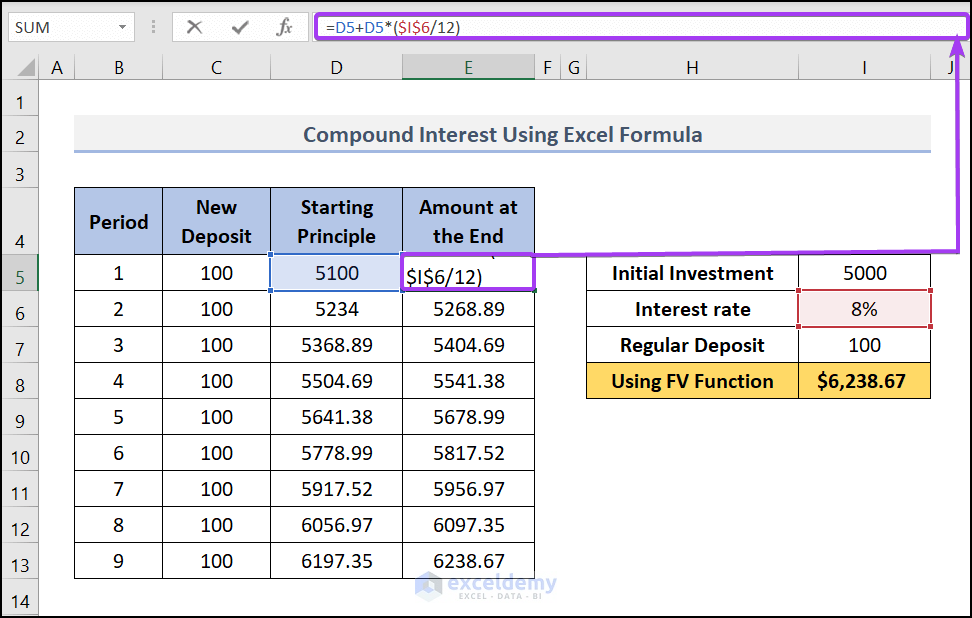
- Later, in the cell E5 (under the column Amount at the End), We have used this formula, E5=D5+D5*($I$6/12)
This formula will add the Starting Principle (D5) to the interest earned (D5*($I$6/12)) for the period. We are dividing the yearly interest rate $I$6 by 12 as the regular deposit is made monthly. Copy the formula and apply it to the cells below.
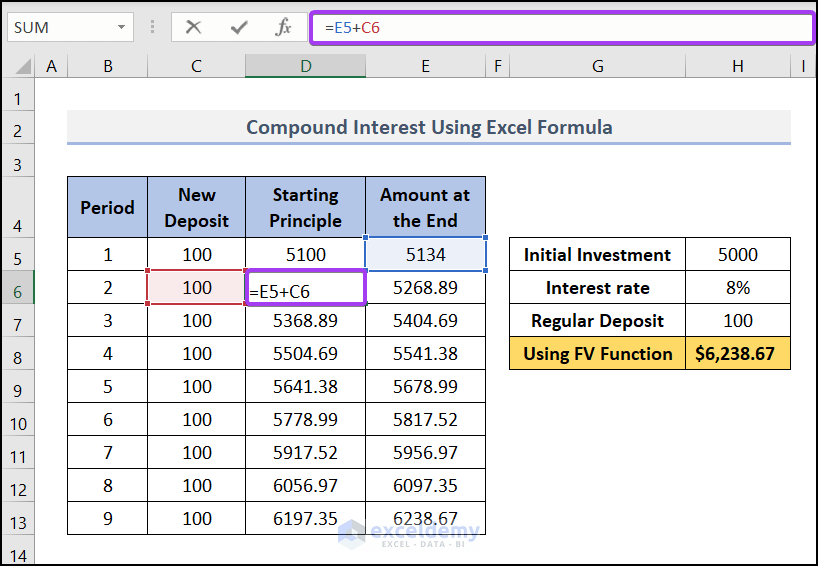
- Then, in cell D6 (under the column Starting Principle), We have used this formula, D6=E5+C6. This formula will add the new deposit to the amount at the end of the previous period. And then we copied down this formula for other cells in the column.
- Finally, drag down the Fill Handle tool for other cells and your result will look like this.
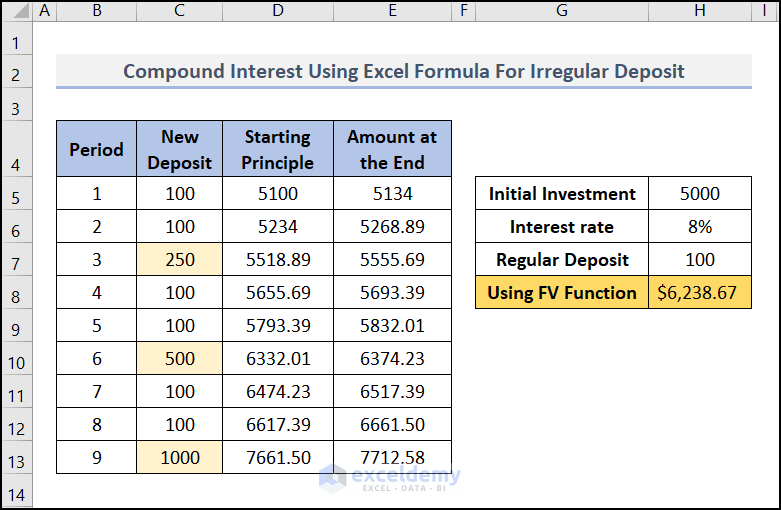
Calculate Compound Interest with Irregular Deposits
However, we can extend the previous template to calculate compound interest with irregular deposits. Just use your irregular deposits manually in the "New deposit" column like the image below.
Definition and Building Compound Interest Formula
Suppose you have some investable money of the amount of $10,000. You go to a bank and the bank said their savings rate is 6% per year. You deposited the money with the bank for the next 3 years as you felt safe with the bank and the interest rate is competitive.
So, your principal is: $10,000
The annual interest rate is: 6%
🔶 After 1 Year:
After 1 year, you will receive interest of amount: $10,000 x 6% = $10,000 x (6/100) = $600
So, after 1 year, your principal + interest will be:
= $10,000 + $600
= $10,000 + $10,000 x 6%; [replacing $600 with $10,000 x 6%]
= $10,000 (1+6%)
If you withdraw this interest ($600), then your principal at the beginning of the 2nd year will be $10,000. But if you don't withdraw the interest, your principal at the beginning of the 2nd year will be $10,000 + $600 = $10,600 And this is where compounding starts. When you don't withdraw the interest, the interest is added to your principal. The principal and earned interest work as your new principal for the next year. Your next year's interest is calculated based on this new principle. Eventually, the yearly return from investments in the coming years gets bigger.
🔶 After 2 Years:
At the beginning of year 2, your new principal is: $10,600
At the end of year 2, you will receive interest (on the basis of new principal) of the amount: of $10,600 x 6% = $636. Let's make the compound interest rate formula from the above expression:
= $10,000(1+6%) + $10,600 x 6%; [replacing $10,600 with $10,000(1+6%) and $636 with $10,600 x 6%] = $10,000(1+6%) + $10,000(1+6%) x 6%; [again replacing $10,600 with $10,000(1+6%)]
= $10,000(1+6%)(1+6%)
= $10,000 x (1+6%)^2
So, we can make a generalized compound interest formula to calculate principal + interest:
Where,
- p is the principal invested at the beginning of the annuity,
- r is the yearly interest rate (APR)
- And n is the number of years.
So, your principal + interest at the end of year 2 will be:
$10600 + $636 = $11,236
We can also reach this same amount using the above formula:
=p(1+r)^n
=$10,000 x (1+6%)^2
= $10,000 (1+0.06)^2
= $10,000 (1.06)^2
=$10,000 x 1.1236
= $11,236
🔶 After 3 Years:
The new principal at the start of year 3 is: $11,236
But we don't need this to calculate the principal + interest at the end of year 3. We can use the formula directly.
After 3 years, your principal + interest will be:
= $10,000 x (1+6%)^3
= $11,910.16
Future Values of an Investment Using Compound Interest Formula
Initially, using the following compound interest formula, we can calculate future values on investment for any compounding frequency.
Where,
- A = Total amount after nt periods
- P = The amount invested at the beginning. It cannot be withdrawn or changed in the investment period.
- r = Annual Percentage Rate (APR)
- n = Number of times interest is compounded per year
- t = Total time in years

Check out the image below. I have shown 4 variations of the above formula.
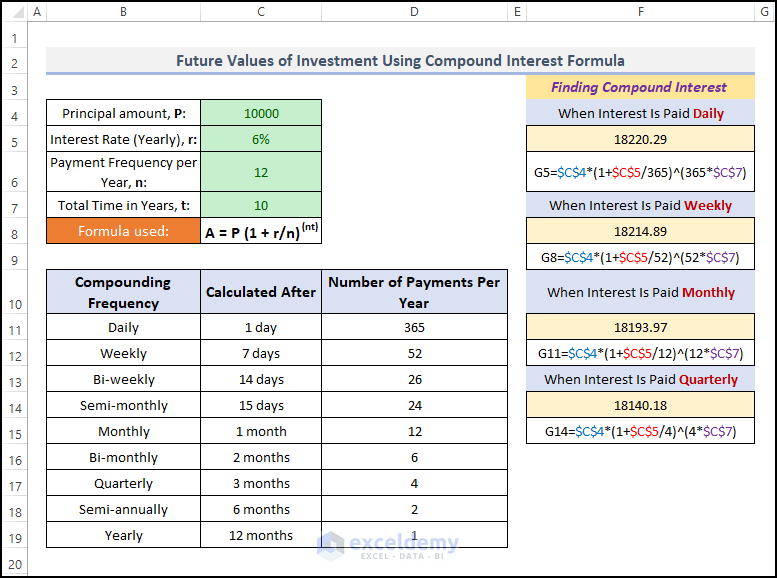
Finally, you see that for the same investment of $10,000, we get the following results:
- For daily compounding: $18220.29
- For weekly compounding: $18214.89
- For Monthly compounding: $18193.97
- And for Quarterly compounding: $18140.18
So, if the number of compounding per year is higher, the return is also higher.
Power of Compounding
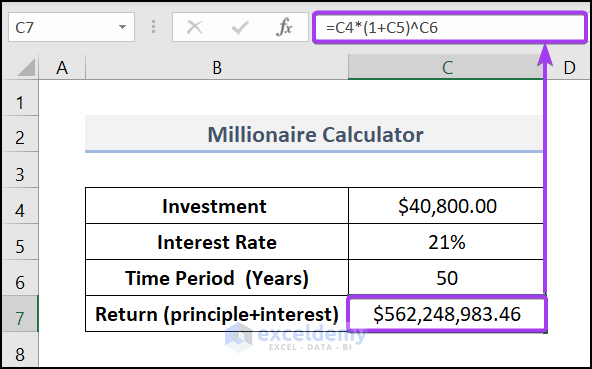
Accordingly, the power of compounding is very significant. Let me show you the power of compounding in the investment world or with your savings.
Let's assume you want to be a millionaire and that is in sleeping mode 😊
Warren Buffet (the living legend of the investment world) advises you to invest in a low-cost index fund, for example, Vanguard 500 Index Investor. And historically this fund has returned 8.33% annual return for the last 15 years (including the fall of 2008).
Practice Section
Here, we have provided a Practice section on each sheet on the right side for your practice. Please do it by yourself.
Conclusion
Basically, understanding the concept of compounding can benefit you hugely. When making investment decisions, you should check out the long-term and consistent growth of your investment. It is far better to earn 15% per year than earn 100% a year and then vanish your investments. Please let us know in the comments section if you have any questions or suggestions. For your better understanding please download the practice sheet. Visit our website Exceldemy , a one-stop Excel solution provider to find out diverse kinds of excel methods. Thanks for your patience in reading this article.
Source: https://www.exceldemy.com/compound-interest-excel-formula-with-regular-deposits/
0 Response to "Excel Value of Continuously Compunded Bond"
Post a Comment